Today, I am going to tell you how to build a simple neural network with JavaScript without using any AI frameworks.

For good understanding you need to know these things:

• OOP, JS, ES6;
• basic math;
• basic linear algebra.

Simple theory

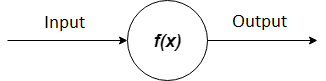
A neural network is a collection of neurons with synapses connected them. A neuron can be represented as a function that receive some input values and produced some output as a result.

Every single synapse has its own weight. So, the main elements of a neural net are neurons connected into layers in specific way.

Every single neural net has at least an input layer, at least one hidden and an output layer. When each neuron in each layer is connected to all neurons in the next layer then it’s called multilayer perceptron (MLP). If neural net has more than one of hidden layer then it’s called Deep Neural Network (DNN).

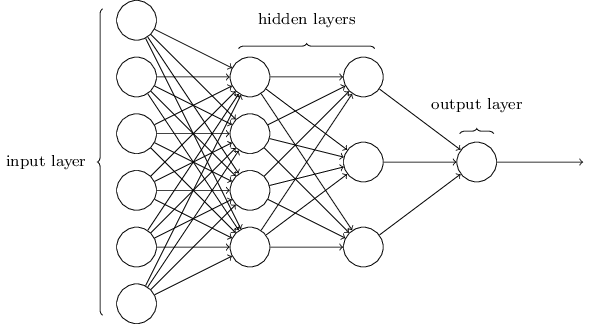
The picture represents DNN of type 6–4–3–1 means 6 neurons in the input layer, 4 in the first hidden, 3 in the second one and 1 in the output layer.

Forward propagation

A neuron can have one or more inputs that can be an outputs of other neurons.

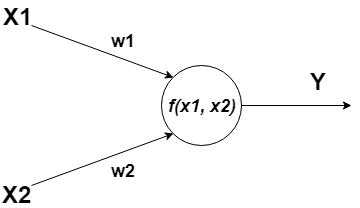
• $X1$ and $X2$  - input data;
• $w1$, $w2$  - weights;
• $f(x1, x2)$  - activation function;
• $Y$ - output value.

So, we can describe all the stuff above by mathematical formula:

The formula describes neuron input value. In this formula: n - number of inputs, x - input value, w - weight, b - bias (w e won’t use that feature yet, but only one thing you should know about that now - it always equals to 1).

As you can see, we need to multiply each input value by its weight and summarize products. We have sum of the products of multiplying x by w. The next step is passing the output value net through activation function. The same operation needs to be applied to each neuron in our neural net.

Finally, you know what the forward propagation is.

Backward propagation (or backpropagation or just backprop)

Backprop is one of the powerful algorithms first introduced in 1970. Read more about how it works.

Backprop consists of several steps you need apply to each neuron in your neural net.

1. First of all, you need to calculate error of the output layer of neural net.

target  -  true value, output  -  real output from neural net.

2. Second step is about calculating delta error value.

$f'$  -  derivative of activation function.

3. Calculating an error of hidden layer neurons.

synapse  -  weight of a neuron that’s connected between hidden and output layer.

Then we calculate delta again, but now for hidden layer neurons.

output  -  output value of a neuron in a hidden layer.

4. It’s time to update the weights.

lrate  -  learning rate.

Buddies, we just used the simplest backprop algorithm and gradient descent 😯. If you wanna dive deeper then watch this video.

And that’s it. We’re done with all math. Let’s just code it!

Practice

So, we’ll create MLP for solving XOR problem. Input, Output for XOR:

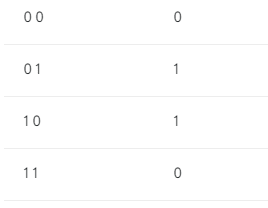
We’ll use Node.js platform and math.js library (which is similar to numpy in Python). Run these commands in your terminal:

mkdir mlp && cd mlp
npm init
npm install babel-cli babel-preset-env mathjs

Let’s create a file called activations.js which will contain our activation functions definition. In our example we’ll use classical sigmoid function (oldschool, bro).

import { exp } from "mathjs";

export function sigmoid(x, derivative) {
  let fx = 1 / (1 + exp(-x));
  if (derivative) return fx * (1 - fx);
  return fx;
}

Then let’s create nn.js file that contains NeuralNetwork class implementation.

import {
  random,
  multiply,
  dotMultiply,
  mean,
  abs,
  subtract,
  transpose,
  add,
} from "mathjs";
import * as activation from "./activations";

export class NeuralNetwork {
  constructor(...args) {
    this.input_nodes = args[0];
    this.hidden_nodes = args[1];
    this.output_nodes = args[2];

    this.epochs = 50000;
    this.activation = activation.sigmoid;
    this.lr = 0.5;
    this.output = 0;

    //generate synapses
    this.synapse0 = random([this.input_nodes, this.hidden_nodes], -1.0, 1.0);
    this.synapse1 = random([this.hidden_nodes, this.output_nodes], -1.0, 1.0);
  }
}

We need to add trainable ability to our network.

train(input, target) {
  for (let i = 0; i < this.epochs; i++) {
    let input_layer = input;
    let hidden_layer_logits = multiply(input_layer, this.synapse0);
    let hidden_layer_activated = hidden_layer_logits.map(v => this.activation(v, false)
    let output_layer_logits = multiply(hidden_layer, this.synapse1);
    let output_layer_activated = output_layer_logits.map(v => this.activation(v, false))

    let output_error = subtract(target, output_layer_activated);
    let output_delta = dotMultiply(output_error, output_layer_logits.map(v => this.activation(v, true)));
    let hidden_error = multiply(output_delta, transpose(this.synapse1));
    let hidden_delta = dotMultiply(hidden_error, hidden_layer_logits.map(v => this.activation(v, true)));

    this.synapse1 = add(this.synapse1, multiply(transpose(hidden_layer), multiply(output_delta, this.lr)));
    this.synapse0 = add(this.synapse0, multiply(transpose(input_layer), multiply(hidden_delta, this.lr)));
    this.output = output_layer;

    if (i % 10000 == 0)
      console.log(`Error: ${mean(abs(output_error))}`);
  }
}

And just add predict method for producing result.

predict(input) {
  let input_layer = input;
  let hidden_layer = multiply(input_layer, this.synapse0).map(v => this.activation(v, false));
  let output_layer = multiply(hidden_layer, this.synapse1).map(v => this.activation(v, false));
  return output_layer;
}

Finally, let’s create index.js file where all the stuff we created above will joined.

import {NeuralNetwork} from './nn' 
import {matrix} from 'mathjs'

const input = matrix([[0,0], [0,1], [1,0], [1,1]]);
const target = matrix([[0], [1], [1], [0]]);

const nn = new NeuralNetwork(2, 4, 1); //
nn.train(input, target);
console.log(nn.predict(input));

Predictions from our neural net:

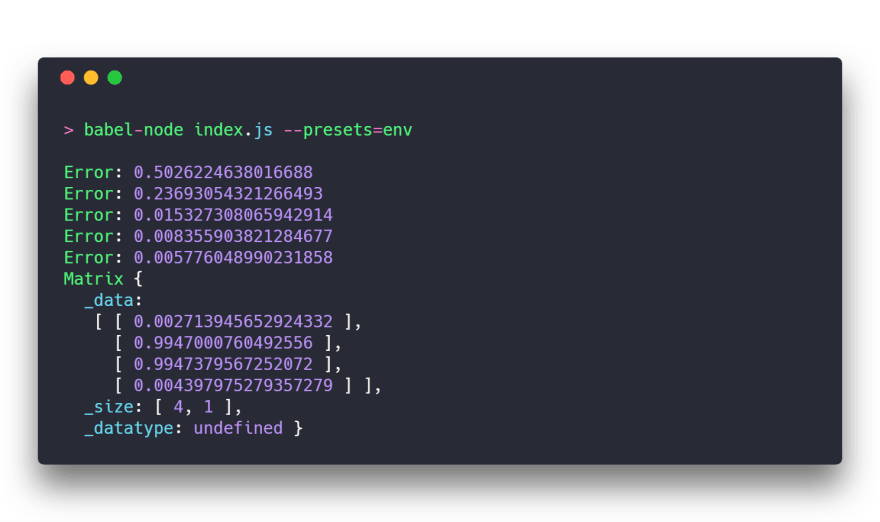
Conclusions

As you can see, the error of the network is going to zero with each next epoch. But you know what? I’ll tell you a secret — it won’t reach zero, bro. That thing can take very long time to be done. It won’t happens. Never.

Finally, we see results that are very close to input data. The simplest neural net, but it works!

Source code is available on my GitHub.

Original article posted on Dev.to.